【人工智能】<吴恩达-机器学习>批量梯度下降&矩阵和向量运算概述
目录一、Gradient descent for liner regression - 线性回归:1.线性回归的梯度下降法:2."Batch" Gradient Descent - 批量梯度下降法:二、Matrices and Vectors - 矩阵和向量:1.Matrix:2.Vector:三、矩阵&向量运算:1.Addition and scalar multiplic....

【机器学习中的矩阵求导】(三)矩阵向量求导(微分法)
一、矩阵微分我们熟悉的标量的微分:二、矩阵微分的性质三、使用微分法求解矩阵向量求导3.1 迹函数的技巧

【机器学习中的矩阵求导】(二)矩阵向量求导(定义法)
假设:x xx表示标量;X XX表示m×n维的矩阵;求导的因变量用y yy表示标量;Y YY表示p × q p×qp×q维矩阵二、用定义法求解标量对向量求导小结:例2的较复杂的实值函数求导,最终排列出的求导结果较为复杂。三、标量对向量求导寻找较复杂的实值函数求导更方便的方法,不是每次都先针对任意一个分量,再进行排列。标量对向量求导的基本法则(PS:和我们以前标量对标量求导的法则类似):常量对向量....
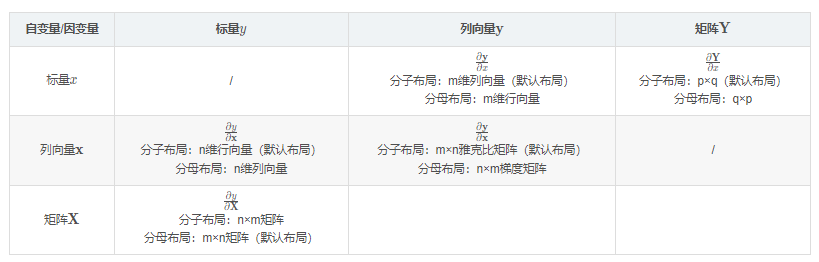
【机器学习中的矩阵求导】(三)矩阵向量求导(微分法)
一、矩阵微分我们熟悉的标量的微分:二、矩阵微分的性质三、使用微分法求解矩阵向量求导3.1 迹函数的技巧四、迹函数对向量矩阵求导常见的迹函数的求导过程:(1)直接根据矩阵微分的定义:

本页面内关键词为智能算法引擎基于机器学习所生成,如有任何问题,可在页面下方点击"联系我们"与我们沟通。
机器学习平台 PAI您可能感兴趣
- 机器学习平台 PAI scikit-learn
- 机器学习平台 PAI python
- 机器学习平台 PAI代码
- 机器学习平台 PAI论文
- 机器学习平台 PAI数字识别
- 机器学习平台 PAI实战
- 机器学习平台 PAI numpy
- 机器学习平台 PAI降维
- 机器学习平台 PAI模型
- 机器学习平台 PAI构建
- 机器学习平台 PAIpai
- 机器学习平台 PAI算法
- 机器学习平台 PAIpython
- 机器学习平台 PAI数据
- 机器学习平台 PAI应用
- 机器学习平台 PAI训练
- 机器学习平台 PAI人工智能
- 机器学习平台 PAI入门
- 机器学习平台 PAI方法
- 机器学习平台 PAI深度学习
- 机器学习平台 PAI分类
- 机器学习平台 PAI平台
- 机器学习平台 PAI笔记
- 机器学习平台 PAI学习
- 机器学习平台 PAI特征
- 机器学习平台 PAI实践
- 机器学习平台 PAI决策
- 机器学习平台 PAIai
- 机器学习平台 PAI部署
- 机器学习平台 PAI网络
