数据结构与算法细节篇之最短路径问题:Dijkstra和Floyd算法详细描述,java语言实现。
前言 最短路径的算法有两个,Dijkstra算法 和 Floyd算法。 Dijkstra算法 解决的是 单源 最短路径问题。 Floyd算法解决的是 多源 最短路径问题,并且可以处理负权图。 今天要讲的就是Dijkstra算法。 加:feng--Insist(大写的i),进java交流群讨论互联网+技术。可索要PPT等资料。 其他资料,建议先看本篇博客。:Dijkstra算法和Fl...

弗洛伊德(Floyd)算法(C/C++)
弗洛伊德算法(Floyd's algorithm),又称为弗洛伊德-沃尔什算法(Floyd-Warshall algorithm),是一种用于在加权图中找到所有顶点对之间最短路径的算法。这个算法适用于有向图和无向图,并且可以处理负权重边,但不能处理负权重循环。 弗洛伊德算法(Floyd-Warshall Algorithm)是一种用于计算图中所有顶点对之间最短路径的动态规划算法。本文将详...
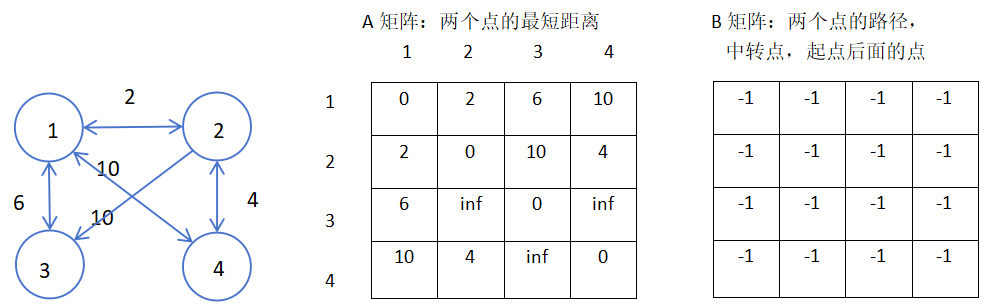
Floyd算法
与迪杰斯特拉算法相似,弗洛伊德算法是一种计算最短路径的问题,与迪杰斯特拉算法不同的是,该算法可计算多源点带权图(可带负权值,但非负周期[1])的最短路径的问题。 以上图为例,介绍如何手写。 首先写出该图的邻接矩阵,记...
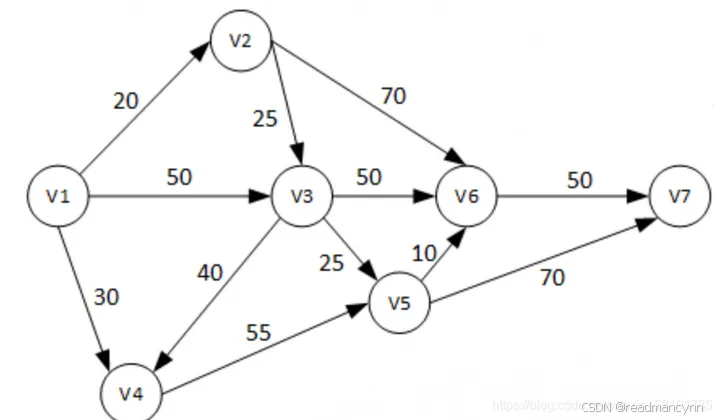
Frogger(Floyd算法)
题目: Freddy Frog is sitting on a stone in the middle of a lake. Suddenly he notices Fiona Frog who is sitting on another stone. He plans to visit her, but since the water is dirty and full of tour...
最短路之Floyd算法
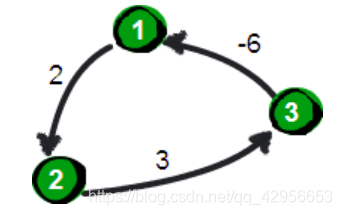
关于原理只有五行的Floyd最短路算法需要注意的是:Floyd算法不能解决带有“负权回路”(或者叫“负权环”)的图,因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中,每绕一次1->-2>3这样的环,最短路就会减少1,永远找....
class065 A星、Floyd、Bellman-Ford与SPFA【算法】
class065 A星、Floyd、Bellman-Ford与SPFA【算法】2023-12-9 19:27:02算法讲解065【必备】A星、Floyd、Bellman-Ford与SPFAcode1 A*算法模版// A*算法模版(对数器验证)package class065; import java.util.PriorityQueue; // A*算法模版(对数器验证) public cla....

Floyd 最短路径【学习算法】
前言2023-9-26 18:09:58以下内容源自《【学习算法】》仅供学习交流使用推荐无Floyd 最短路径public class FloydAlgorithm { private static final int INF = 99999; public void floyd(int[][] graph, int n) { int[][] dist = new...
floyd算法
弗洛伊德算法(Floyd’s algorithm),也被称为弗洛伊德-沃舍尔算法(Floyd-Warshall algorithm),是一种用于解决图中所有节点对之间最短路径的动态规划算法。该算法可以在有向图或带权无向图中找到所有节点之间的最短路径。它的核心思想是通过所有中间节点逐步迭代来更新每对节点之间的最短路径。具体的步骤如下:初始化一个矩阵,矩阵的每个元素代表从一个节点到另一个节点的最短路....
Floyd算法的应用
Floyd算法的证明void floyd()//三层循环实现floyd算法 { for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) d[i][j]=min(d[i][j],d[i][k]+d[k][j]); } Floyd的运用 1.牛...

转:用一个例子说明Floyd算法
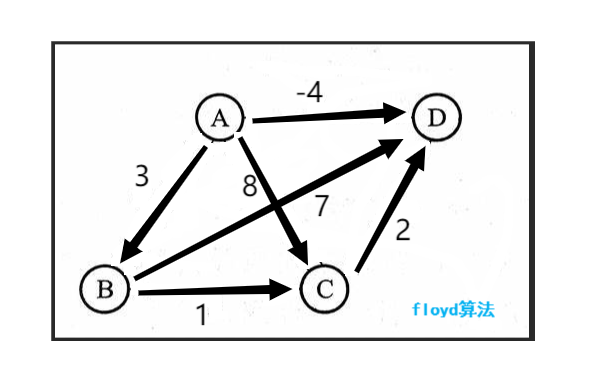
弗洛伊德算法(Floyd's algorithm)是一种用于求带权图中最短路径的算法,适用于带有正负权边的图(但不能有负环)。这种算法也有时被称为弗洛伊德-沃尔什算法。该算法基于动态规划,其时间复杂度为O(V^3),其中V是图中的顶点数。此外,该算法还可用于检测图中的负环并求出传递闭包。 下面是一个使用弗洛伊德算法求图中所有顶点对之间最短路径的示例:假设我们有一个具有4个顶点(A,B,C和D).....
本页面内关键词为智能算法引擎基于机器学习所生成,如有任何问题,可在页面下方点击"联系我们"与我们沟通。
智能引擎技术
AI Online Serving,阿里巴巴集团搜推广算法与工程技术的大本营,大数据深度学习时代的创新主场。
+关注

