Python语言如何使用MindOpt建模并求解二次规划问题
本篇文章是系列文章的第三篇,下文小编首先分享个人对二次规划定义的理解,然后举一个例题,最后使用 MindOpt Python 语言的 API 来建模以及求解 二次规划问题示例 中的问题以及展示求解的结果。MindOpt Python、C、C++语言求解LP、MILP、QP问题系列Python: 线性规划LP问题、混合整数线性规划MILP问题、二次规划QP问题(本篇)C ....
Python之建模规划篇--非线性规划
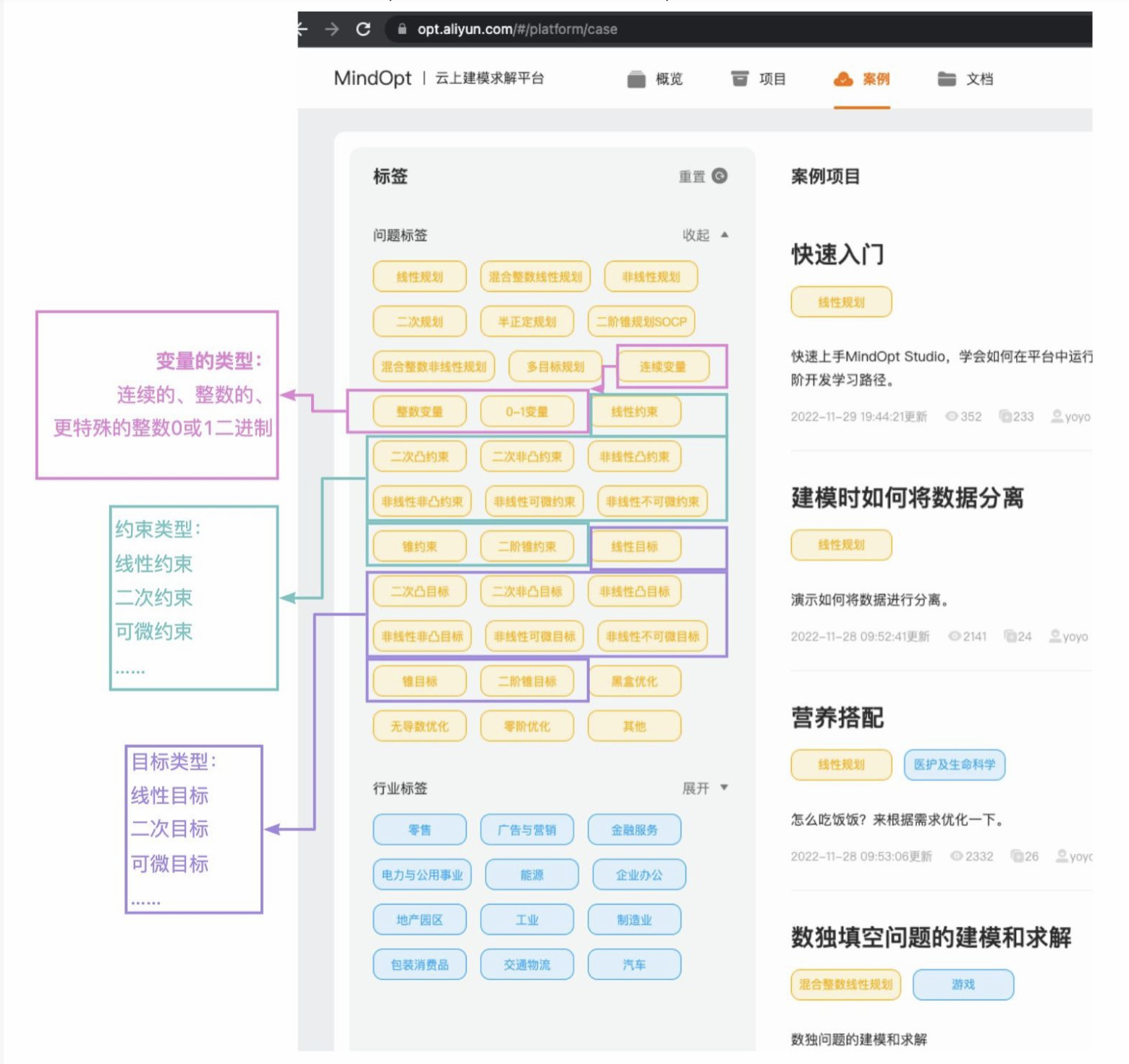
基本介绍如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。一般说来,解非线性规划要比解线性规划问题困难得多。而且,也不象线性规划有单纯形法这一通用方法,非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。这是一个非线性规划问题的一般形式对于一个实际问题,在把它归结成非线性规划问题时,一般要注意如下几点:(i)确定供选方案:首先要收集同问题有关的资料....

Python之建模规划篇--整数规划
基本介绍规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法,往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。整数规划的分类如不加特殊说明,一般指整数线性规划。对于整数线性规划模型大致可分为两类:变量全限制为整数时,称纯(完全)整数规划。变量部分限制为整数的,称混合整数规划。整数规划的特....

Python之建模规划篇--线性规划
基本介绍在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划,而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947 年G. B. Dantzig 提出求解线性规划的单纯形方法以来,线性规划在理论上趋向成熟,在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策....
本页面内关键词为智能算法引擎基于机器学习所生成,如有任何问题,可在页面下方点击"联系我们"与我们沟通。
