[深度学习实战]基于PyTorch的深度学习实战(中)[线性回归、numpy矩阵的保存、模型的保存和导入、卷积层、池化层](二)
5.2 Conv1d conv1d 是一维卷积,它和 conv2d 的区别在于只对宽度进行卷积,对高度不卷积。5.2.1 函数定义torch.nn.functional.conv1d(input, weight, bias=None, stride=1, padding=0, dilation=5.2.2 参数说明 input:输入的Tensor数据,格式为 (batc....
![[深度学习实战]基于PyTorch的深度学习实战(中)[线性回归、numpy矩阵的保存、模型的保存和导入、卷积层、池化层](二)](https://ucc.alicdn.com/pic/developer-ecology/u4n2puyxrj26a_230871bbe1ee46428c2311a4c06971d9.png)
[深度学习实战]基于PyTorch的深度学习实战(中)[线性回归、numpy矩阵的保存、模型的保存和导入、卷积层、池化层](一)
一、前言 本想着一篇博文直接写完基于PyTorch的深度学习实战,可写着写着发现字数都上万了。考虑到读者可能花了大力气对这么一篇博文看到失去了对PyTorch神经网络的耐心,同时也为了我个人对文章排版的整理,还是分成了分卷阅读。 这里贴一下上篇博文:[深度学习实战]基于PyTorch的深度学习实战(上)[变量、求导、损失函数、优化器]二、线性回归 线性回归也叫....
![[深度学习实战]基于PyTorch的深度学习实战(中)[线性回归、numpy矩阵的保存、模型的保存和导入、卷积层、池化层](一)](https://ucc.alicdn.com/pic/developer-ecology/u4n2puyxrj26a_7141a9e5a75741ad8cc99cc4720add8a.png)
《深度学习500问》张量和矩阵的区别
从代数角度将,矩阵是向量的推广。向量可以看成一维的“表格”(即分量按照顺序排成一排),矩阵可以看成二维的“表格”(分量按照纵横位置排列),n阶张量可以看成n维的“表格”。张量的严格定义是利用线性映射来描述的。从几何角度讲:矩阵是一个真正的几何量。也就是说,它是一个不随参照系坐标变换而变化的量。向量也具有这种特性。某些条件下,张量可以用矩阵来表达。表示标量的数和表示向量的三维数组也可以分别称作1x....
深度学习核对矩阵的维数对w权重矩阵的维数的计算
(n,m):n为神经节点数,m为样本数由上图我们可以设几个例子: 已知:可知x可以看做是a^[0]已知:可知:分析第一个例子,由行列矩阵相乘理解因为z是(3,1)的,而x是(2,1)的,要变成z(3,1),w只能是(3,2)。因此可得结论(建议直接记) :
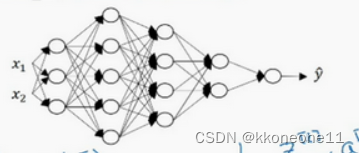
优达学城深度学习之二——矩阵数学和Numpy复习
PS:由于第一篇介绍Anaconda的文章不能申请原创标志故发表不了,所以先发表第二篇文章,第一篇会改一些再发表出来。一、数据维度维度(scalar),张量(Tensor)。3表示零维张量,[1 2 3]表示一维张量,矩阵表示二维张量,任何大于二维张量就叫张量(Tensor)。如下图所示:二、Numpy简介2.1、NumPy 中处理数字的常见方式是通过 ndarray 对象。它们与 Python....

受限波尔茨曼机RBM_DBN深度学习网络训练和测试matlab仿真,数据库为随机数矩阵
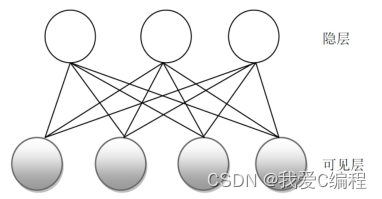
1.算法概述 受限波尔兹曼机(Restricted Boltzmann Machines,RBM)是一类具有两层结构、对称连接且无自反馈的随机神经网络模型,层间全连接,层内无连接。我们知道玻尔兹曼机的是全连接的,其结构如下图所示: 受限玻尔兹曼机是玻尔兹曼机(Boltzman machine,BM)的一种特殊拓扑结构。BM的原理起源于统计物理学,是一种基于能量函数的建模方法,能够描述变量...
深度学习基础:标量、向量、矩阵、张量
深度学习基础:标量、向量、矩阵、张量标量(scalar)标量是一个独立存在的数,比如线性代数中的一个实数5就可以被看作一个标量,所以标量的运算相对简单,与平常做的算数运算类似。向量(vector)向量指一列顺序排列的元素,我们通常习惯用括号将这些元素扩起来,其中每个元素都又一个索引值来唯一的确定其中在向量中的位置。矩阵(matrix)矩阵是二维数组,其中的每一个元素被两个索引而非一个所确定,我们....
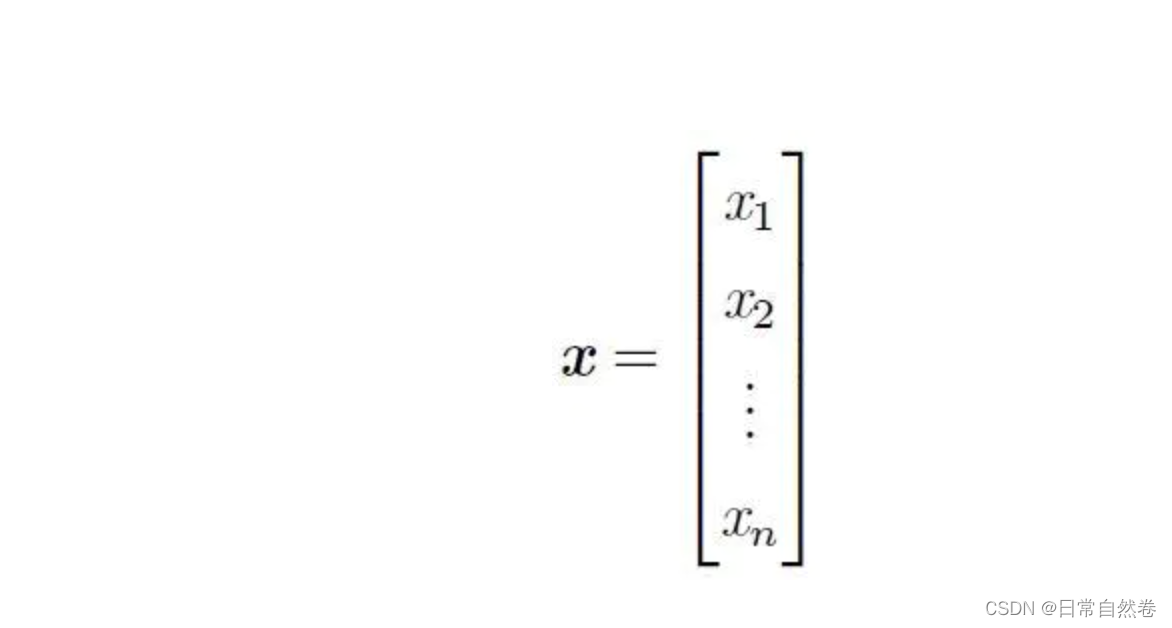
一文读懂深度学习中的矩阵微积分,fast.ai创始人&ANTLR之父出品 | 免费资源
想要真正了解深度神经网络是如何训练的,免不了从矩阵微积分说起。 虽然网络上已经有不少关于多元微积分和线性代数的在线资料,但它们通常都被视作两门独立的课程,资料相对孤立,也相对晦涩。 不过,先别打退堂鼓,来自旧金山大学的Terence Parr教授说:矩阵微积分真的没有那么难。 这位ANTLR之父和fast.ai创始人Jeremy Howard一起推出了一篇免费教程,旨在帮你快速入门深度学习中的矩....

深度学习应用系统分析:应用组合和形态矩阵找到正确路径
对深度学习研究和应用的兴趣从未这么热过。深度学习最迷人的地方是,神经网络似乎能够解决以前只能用定制方法解决的各种问题。 【导读】本文收录了arXiv.org上关于深度学习的一些最新的研究论文,列出了这些文章的内容,包括“深度学习八大灵感应用”、“深度学习用例”、“科学与工程中的深度学习应用”、“深度学习应用程序的下一次浪潮”等。针对这些文章缺乏系统方法的问题,提出了具体的组合矩阵、形态...

本页面内关键词为智能算法引擎基于机器学习所生成,如有任何问题,可在页面下方点击"联系我们"与我们沟通。
智能搜索推荐
智能推荐(Artificial Intelligence Recommendation,简称AIRec)基于阿里巴巴大数据和人工智能技术,以及在电商、内容、直播、社交等领域的业务沉淀,为企业开发者提供场景化推荐服务、全链路推荐系统开发平台、工程引擎组件库等多种形式服务,助力在线业务增长。
+关注
